Omega Group - Pay Discrimination

Relationship Salary - Gender ?

The data frame omega contains the salaries for the sample of 50 executives in the company. Can we conclude that there is a significant difference between the salaries of the male and female executives?

Note that we can perform different types of analyses, and check whether they all lead to the same conclusion

. Confidence intervals . Hypothesis testing . Correlation analysis . Regression

We calculate summary statistics on salary by gender. Also, create and print a dataframe where, for each gender, we show the mean, SD, sample size, the t-critical, the SE, the margin of error, and the low/high endpoints of a 95% condifence interval

# Summary Statistics of salary by gender
mosaic::favstats (salary ~ gender, data=omega)

##   gender   min    Q1 median    Q3   max  mean   sd  n missing
## 1 female 47033 60338  64618 70033 78800 64543 7567 26       0
## 2   male 54768 68331  74675 78568 84576 73239 7463 24       0

# Dataframe with two rows (male-female) and having as columns gender, mean, SD, sample size, 
# the t-critical value, the standard error, the margin of error, 
# and the low/high endpoints of a 95% confidence interval

gender_salary <- omega %>%
  group_by(gender) %>%
  select(salary) %>%
  summarise(mean_sal = mean(salary),
            stdev_sal = STDEV(salary),
            sample_size_sal = n(),
            stder_sal = stdev_sal/ sqrt(n())) %>%
  mutate(t_critical = qt(0.975, sum(sample_size_sal)-1),
         SE_sal = stder_sal/sqrt(sample_size_sal),
         margin_of_error = t_critical*SE_sal,
         lower_bound_CI_sal = mean_sal - (1.96*stder_sal),
         upper_bound_CI_sal = mean_sal + (1.96*stder_sal))

From the analysis above, we can conclude that the difference between the relationships of salary and gender is at least 95% statistically significant. The confidence intervals of salaries of men and women do not overlap and there is an observed difference of about £10 000, leading us to an initial observation that there is gender discrimination happening.

We can also run a hypothesis testing, assuming as a null hypothesis that the mean difference in salaries is zero, or that, on average, men and women make the same amount of money. We tun your hypothesis testing using t.test() and with the simulation method from the infer package.

# hypothesis testing using t.test() 
t.test(salary ~ gender, data = omega)

## 
##  Welch Two Sample t-test
## 
## data:  salary by gender
## t = -4, df = 48, p-value = 2e-04
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
##  -12973  -4420
## sample estimates:
## mean in group female   mean in group male 
##                64543                73239

# hypothesis testing using infer package
infer_gender_salary <- omega %>%
  specify(salary ~ gender) %>%
  calculate(stat = "diff in means", order = c("male", "female"))

null_dist <- omega %>%
  # specify variables
  specify(salary ~ gender) %>%
  
  # assume independence, i.e, there is no difference
  hypothesize(null = "independence") %>%
  
  # generate 1000 reps, of type "permute"
  generate(reps = 1000, type = "permute") %>%
  
  # calculate statistic of difference, namely "diff in means"
  calculate(stat = "diff in means", order = c("male", "female"))

The t-stat for our hypothesis test is -4, which is more than our boundary of 2/-2. This leads us to reject the null hypothesis. Additionally, our p-value is less than 5%, which means that we are not likely to get a sampling error in our data. So we can assume that our alternative hypothesis is right, ie. that there is a difference between the salaries of males and females.

Relationship Experience - Gender?

At the board meeting, someone raised the issue that there was indeed a substantial difference between male and female salaries, but that this was attributable to other reasons such as differences in experience. A questionnaire send out to the 50 executives in the sample reveals that the average experience of the men is approximately 21 years, whereas the women only have about 7 years experience on average (see table below).

# Summary Statistics of experience by gender
favstats (experience ~ gender, data=omega)

##   gender min    Q1 median   Q3 max  mean    sd  n missing
## 1 female   0  0.25    3.0 14.0  29  7.38  8.51 26       0
## 2   male   1 15.75   19.5 31.2  44 21.12 10.92 24       0

gender_experience <- omega %>%
  group_by(gender) %>%
  select(experience) %>%
  summarise(mean_exp = mean(experience),
            stdev_exp = STDEV(experience),
            sample_size_exp = n(),
            stder_exp = stdev_exp/ sqrt(n())) %>%
  mutate(t_critical = qt(0.975, sum(sample_size_exp)-1),
         SE_exp = stder_exp/sqrt(sample_size_exp),
         margin_of_error = t_critical*SE_exp,
         lower_bound_CI_exp = mean_exp - (1.96*stder_exp),
         upper_bound_CI_exp = mean_exp + (1.96*stder_exp))

Based on this evidence, can we conclude that there is a significant difference between the experience of the male and female executives? Let’s perform similar analyses as in the previous section. Does our conclusion validate or endanger our conclusion about the difference in male and female salaries?

From the analysis above, we can conclude that the difference between experience levels of males and females is at least 95% statistically signifcant. This endangers our initial conclusion that the difference in salaries between genders is solely due to discrimination. However, more analysis needs to be conducted before we can form a final conclusion.

Relationship Salary - Experience ?

Someone at the meeting argues that clearly, a more thorough analysis of the relationship between salary and experience is required before any conclusion can be drawn about whether there is any gender-based salary discrimination in the company.

We analyse the relationship between salary and experience and draw a scatterplot to visually inspect the data.

ggplot(omega, aes(x=salary, y = experience))+
  geom_point()+
  geom_smooth(color="red") +
  theme_bw() +
  labs (
    title = "Salary by Experience"
  )

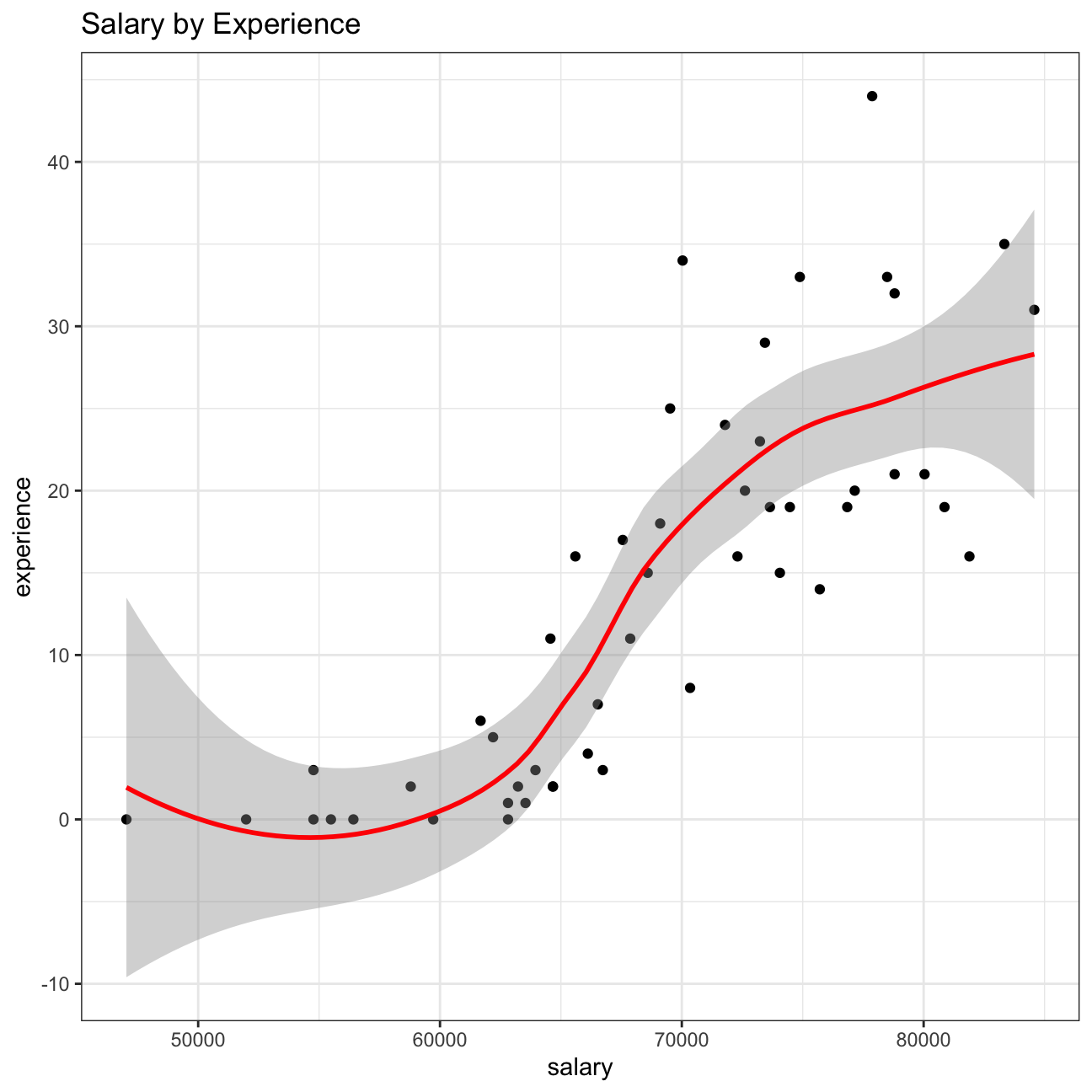
From the scatterplot above, we can see a clear correlation between salary and experience. This would confirm the argument that salary is related to experience, and reject the argument that salary is related to gender. At this point of the analysis, we could say that there is just insufficient information to tell whether there is any gender-based salary discrimination, as it seems to be more related to experience.

Check correlations between the data

We use GGally:ggpairs() to create a scatterplot and correlation matrix. Essentially, we change the order our variables will appear in and have the dependent variable (Y), salary, as last in our list. We then pipe the dataframe to ggpairs() with aes arguments to colour by gender and make ths plots somewhat transparent (alpha = 0.3).

omega %>% 
  select(gender, experience, salary) %>% #order variables they will appear in ggpairs()
  ggpairs(aes(colour=gender, alpha = 0.3))+
  theme_bw()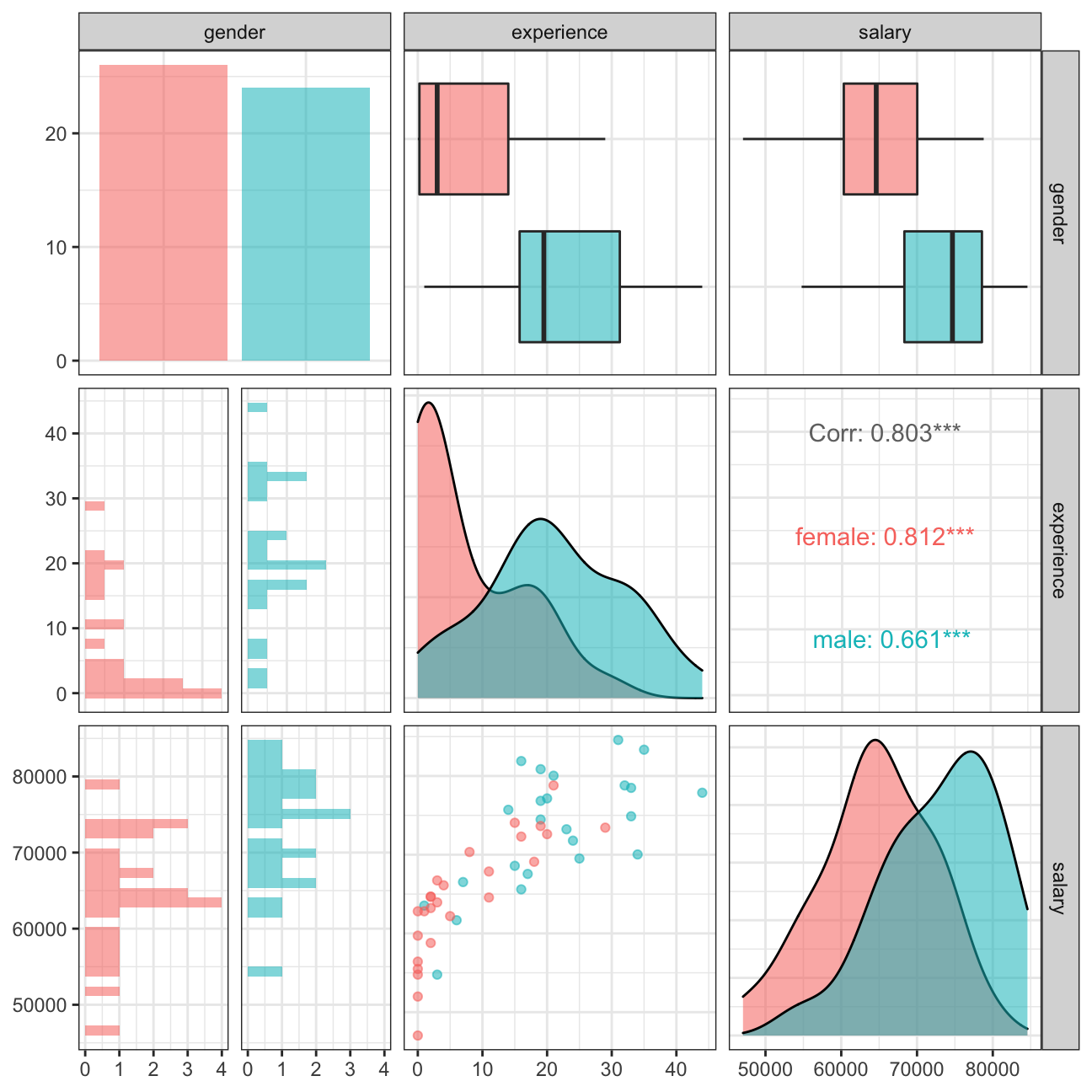

This salary-experience plot, organized by gender, tells us a lot. From the bottom-left of the plot, which concern employees with minimum experience, we can infer that women actually have higher salaries than men. However, as we move towards the upper-middle part of the plot, we can see that women with 15-30 years of experience are paid less than their male peers. Additionally, employees witht the most experience in the company (30-45 years), are solely male, and thus there is no way to tell whether there is any gender-based salary discrimination going on. However, it may be possible that for these senior roles, only males have been considered, as there is no woman with this much experience in this company. This would introduce another gender-based discrimination into the mix.